There’s a lot of glib talk about how technology–ranging from ride-hailing services like Uber and Lyft, to instrumented Smart Cities and, ultimately, autonomous vehicles–will fundamentally reshape urban transportation. We’re told, for example, that autonomous vehicles will eliminate traffic fatalities, obviate the need for parking lots, and solve transit’s “last mile” problem. But there are good reasons to be skeptical.
As Jarrett Walker has famously pronounced, these would-be alternatives have a geometry problem. Solutions that rely upon trying to put more travelers in lots of smaller, often single-occupancy vehicles will inevitably run out of space in urban environments. In Walker’s view, the space efficiency of mass transit–city buses and rail lines–makes them the only feasible way of moving large numbers of people into, out of, and around big cities.
So a bus with 4o people on it today is blown apart into, what, little driverless vans with an average of two each, a 20-fold increase in the number of vehicles? It doesn’t matter if they’re electric or driverless. Where will they all fit in the urban street? And when they take over, what room will be left for wider sidewalks, bike lanes, pocket parks, or indeed anything but a vast river of vehicles?
No amount of technology can overcome the limits imposed by simple geometry.
There’s a lot of merit to this view. And too little thought has been given to how technological solutions might actually scale in actual urban environments. Even in New York City, with very sophisticated instrumentation of the taxi fleet and copious reports of activity from Uber and Lyft, there’s actually no comprehensive assessment of how the growth of these services has affected travel times and congestion, according to Charles Komanoff.
While the geometry problem is real, and under-appreciated, we think these new technological solutions will have to simultaneously face another problem, which we call the “camel problem.” The demand for urban transportation is not simple and linear. Walker’s geometry point is that demand for transportation has an important spatial component. To that we would add that it also has a temporal (time-based) component as well, one that’s well illustrated by our friend, below:

Like the famous Bactrian camel, urban travel demand has has two humps. There’s a peak travel hour in the morning and a second one in the evening in virtually every large city in the US (and most places around the world). It seems to be a regular systemic feature of human activity: we sleep and eat in one set of places, and work, study, shop, and socialize in a different set of places, and disproportionately tend to make trips between these sets of places at the same hours of the day. There’s an abundance of data on this point. Transportation scholars (Tony Downs’ Still Stuck in Traffic is the definitive guide) and traffic engineering text books have documented it for decades. We observed it by pointing a Placemeter camera outside the window of City Observatory’s offices. And the latest bit of evidence for the “camel” view of transportation comes from New York City’s bike share program. Our friends at New York City Economic Development Corporation have an excellent report summarizing some of the trip data from the CitiBike program, showing, among other things the average age of riders (skewing towards young adults), and the most frequent routes traveled (more scenic routes along the West Side, and places not well-served by subways, among others). But the most interesting chart shows when people are riding CitiBikes, by hour of the day. It’s a camel, too:
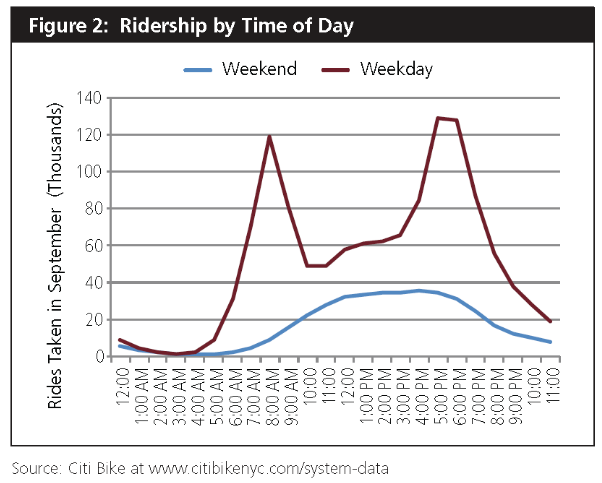
Just as with other modes of transportation (whether it’s the subway, city streets and bridges, or the bus system), travel exhibits two distinct peaks, one corresponding to the morning travel period, and a second in the late afternoon. About twice as many bikes are in use in the morning and afternoon peak hours as in the middle of the day.
The “camel” of urban transportation demand has important implications for designing and operating any new system of getting around cities. For example, a fleet of self-driving cars sized to meet peak hour demand would be more than 50 percent idle during most of the day. Except for an hour or two in the morning and perhaps two to three hours in the late afternoon, most vehicles would be idle.
While we think that there is merit to both the Jarrett Walker “geometry problem” and our own “camel problem,” it’s actually the case that the camel problem trumps geometry. The urban transportation system doesn’t have a geometry problem at 2AM, or indeed most of the day. The geometry problem becomes a problem chiefly in peak hours. Walker is almost certainly correct that geometry will guarantee that solutions like fleets of self-driving cars will never have the capacity to handle traffic loads–during peak hours. But the off-peak hours are a different situation. It seems almost certain that operators of fleets of self-driving cars will use surge-pricing to manage demand (and reap profits) associated with peak hour travel. The competitive challenge for transit is likely to be that fleets of self-driving cars will have abundant capacity during off-peak hours, and they will likely be tempted to offer discounted fares for vehicles that might otherwise be idle (and would probably also cross-subsidize the cost of these trips from profits earned at the peak). As we reported earlier, the best current estimates suggest that self-driving vehicles may cost an average of 30 to 40 cents per mile to operate. It seems likely that the price charged may be higher at the peak, but then discounted from that amount for off-peak hours. That’s a price point that many transit operators would be hard pressed to match.
It’s tempting to visualize alternatives to current transportation systems as a one-traveler or one vehicle-at-a-time problem. But the urban transportation problem is not so much about individual vehicles and trips, as the way trips cumulate in both space and time. The problem is complex one, and will defy simple solutions. Geometry–and camels–will be with us for the foreseeable future.
